Статьи » Акустика
Расчет «Виброплаты», ЗЯ, ФИ, ПИ и ПАС
В статье предлагается модель и программа для расчета «Виброплаты» с портом фазоинвертора (ФИ). При желании порт можно удалить (задать отверстие бесконечно малым). Для ФИ возможно регулировать акустическое трение, что позволяет также рассчитать такое оформление, как ПАС (другое название – «вариовент»).
Кроме того, модель позволяет превратить «Виброплату» в пассивный излучатель (ПИ), выключив формально взаимные силы между «виброплатой» и катушкой динамика. Для этого достаточно в приведенных ниже уравнениях (и файле программы) положить коэффициент связи k=0.
Единицы измерения.
По тексту используется система единиц СИ. Основные параметры динамика выражаются в этих величинах:
[Cms]=м/Н - гибкость подвеса ,
[Rms]=кг/с - механические потери в подвесе,
[Mms]=кг - масса диффузора,
[Sd]=кв.метр - площадь диффузора.
Электрические величины измеряются в вольтах, амперах, омах, теслах, кулонах и фарадах.
Для комплексных величин выбрана зависимость от времени в виде 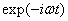 .
В некоторых работах используют частоту со знаком плюс. В этом случае в комплексных выражениях в данной статье необходимо поменять знак у мнимой части на противоположный.
.
В некоторых работах используют частоту со знаком плюс. В этом случае в комплексных выражениях в данной статье необходимо поменять знак у мнимой части на противоположный.
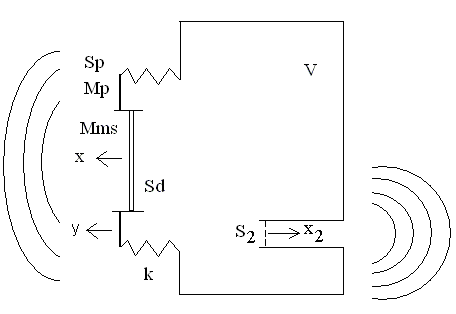
Рис. 1
Модель.
На рис. 1 показан ящик с трубой, в котором колеблется диффузор массы Mms, имеющий площадь Sd, установленный в подвижной пластине. Будем считать, что диффузор движется не изгибаясь как поршень. На диффузор действует сила упругости подвеса, пропорциональная смещению относительно корзины:
cила упругости подвеса = −(x-k×y)/Cms,
где 1/Cms – коэффициент пропорциональности, (величина Cms называется гибкостью подвеса), а k=1 коэффициент, смысл которого дан в введении.
Внешней силой является сила Ампера, возникающая под действием тока в магнитном поле:
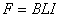 ,
где I – величина тока в катушке, B×L – произведение магнитного поля на длину провода в катушке (Ампер×метр).
,
где I – величина тока в катушке, B×L – произведение магнитного поля на длину провода в катушке (Ампер×метр).
По аналогии с силой трения, потери в подвесе представляются как скорость, умножить на коэффициент пропорциональности Rms.
Пусть диффузор сместился на величину x относительно начального положения, пластина сместилась на величину у, а воздух в трубе переместился на величину x2 (см. Рис. 1).
Адиабатическое изменение давления воздуха внутри ящика связано с изменением объема и величинами смещений следующим образом:
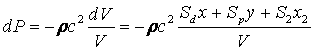 ,
где ρ - плотность воздуха, c – скорость звука, Sd и S2 - площади диффузора, и сечения трубы. Изменение давления приводит к дополнительной силе, действующей на диффузор, равной произведению изменения давления на площадь диффузора (с наружной стороны диффузора для простоты давление воздуха считаем пока постоянным и равным атмосферному).
,
где ρ - плотность воздуха, c – скорость звука, Sd и S2 - площади диффузора, и сечения трубы. Изменение давления приводит к дополнительной силе, действующей на диффузор, равной произведению изменения давления на площадь диффузора (с наружной стороны диффузора для простоты давление воздуха считаем пока постоянным и равным атмосферному).
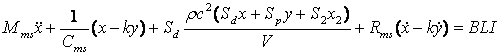 . . |
(1) |
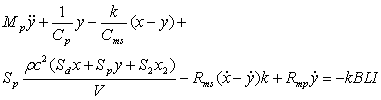 , , |
(2) |
Обозначим объемные смещения как:
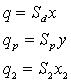 , , |
(3) | |
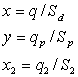 . . |
(3`) |
Разделим уравнение (1) на Sd с учетом (3):
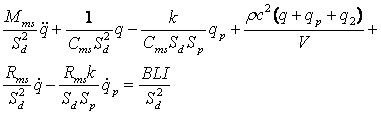 , , |
(4) |
Аналогично для уравнения (2) после деления на Sp:
 . . |
(5) |
Сила тока определяется из уравнения, в которое входит относительное смещение диффузора по отношению к пластине (т.е. величина x-y):
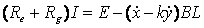 . . |
(6) |
В результате уравнения движения диффузора и пластины будут иметь вид:
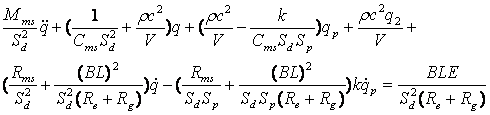 , , |
(7) |
 . . |
(8) |
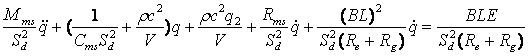 .
.
Будем далее использовать Фурье-анализ, и рассмотрим одну гармонику сигнала заданной частоты. Для гармонических колебаний взятие производной равносильно умножению на круговую частоту, т.е.
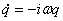 ,
,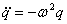 .
Чтобы «замкнуть» систему уравнений, необходимо связать давление на входе трубы с объемной скоростью в трубе. По определению, эта связь выражается через акустическое сопротивление:
.
Чтобы «замкнуть» систему уравнений, необходимо связать давление на входе трубы с объемной скоростью в трубе. По определению, эта связь выражается через акустическое сопротивление: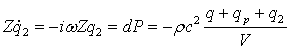 , , |
(9) |
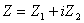 . . |
(10) |
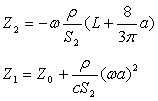 , , |
(11) |
В результате окончательно получаем линейную систему трех уравнений относительно q, q2 и qp:
  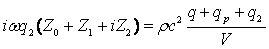 |
(12) |
Компьютерная программа.
Можно выписать общее решение системы (12), однако оно довольно громоздко. Удобнее воспользоваться мощным вычислительным пакетом Mathematicа, который позволяет решать уравнения в символьном виде и строить графики. Уравнения (12) были введены в эту программу, можно скачать соответствующий файл.
Зачем был нужен коэффициент k=1 в уравнениях? Его смысл – превратить модель в модель ПИ. Для этого надо положить в файле программы k=0. Этот коэффициент учитывает взаимное взаимодействие между диффузором и пластиной через электромагнитную силу, силу упругости подвеса динамика и трение в нем. Если выключить это взаимодействие, то пластина будет эквивалентна ПИ.
Пример "Закрытый ящик".
В предельном случае (масса пластины равна бесконечности, гибкость подвеса равна нулю) – должно получатся решение, соответствующее обычной системе типа ЗЯ или ФИ.
Выполним для этого случая расчет на примере динамика JBL 123A:
V=0.160 [куб. метр] - объем колонки;
ρ=1.2 [кг/куб. метр] - плотность воздуха;
c=340 [м/c] - скорость звука.
Параметры динамика:
Mms=0.056 [кг];
Cms=0.00071 [метр/ньютон];
Rms=1.27 [Ньютон×сек/метр];
B×L=9.8 [Тл×метр];
Sd=0.049 [кв м] - площадь диффузора;
Re=5.5 [Ом] - сопротивление катушки;
Rg=0 [Ом] - выходное сопротивление источника.
Параметры пластины:
Mp=3 [кг] - масса с учетом корзины динамика;
Cp=0.000000000000000000000000002 [метр/ньютон] - подвижность относительно корпуса (такое малое значение означает бесконечную жесткость подвеса пластины).
k=0;
Z0=0 - потери на трение в порту.
Rmp=1 [Ньютон*сек/ метр] - потери в подвесе;
Sp=0.2 [кв м] - площадь излучающей поверхности.
L=0.1 [м] - длина порта;
a=0.00000000000000000000000001 [м] - радиус порта (такое малое значение означает отсутствие порта).
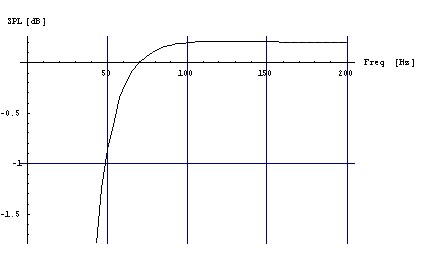
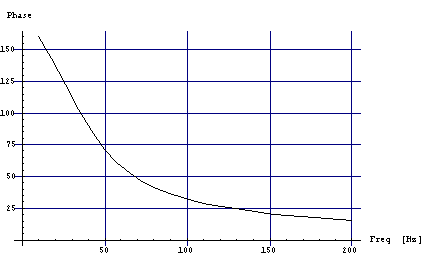
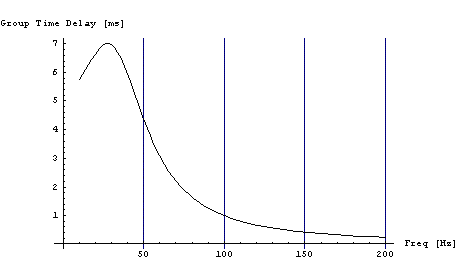
Рис.2 ЗЯ объемом 160 литров.
Пример расчета "Виброплаты".
Далее перейдем к расчету непосредственно подвижной пластины.
Увеличим гибкость подвеса виброплаты относительно корпуса Cp=0.0002:
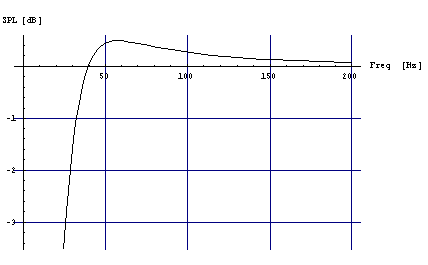
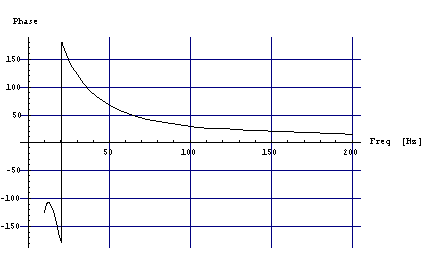
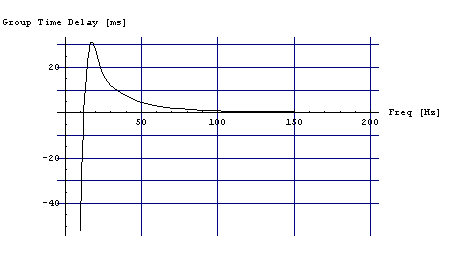
Рис. 3 АЧХ, ФЧХ и ГВЗ для системы динамик на подвижной пластине, V=160 литров.
Заметно добавление баса на НЧ (по сравнению с Рис.2) . Но ГВЗ стало хуже.
Сравнение "Виброплаты" с ФИ.
Попробуем «вытянуть» бас обычным образом с помощью ФИ и сравним результат с «Виброплатой».
L=0.1 [м] - длина порта;
a=0.05 [м] - радиус отверстия порта;
V=0.4
Cp=0.000000000000000000000000000000000002 - (эффект «Виброплаты» выключен – подвижность пластины равна нулю).
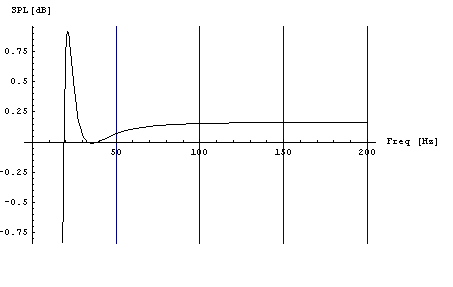
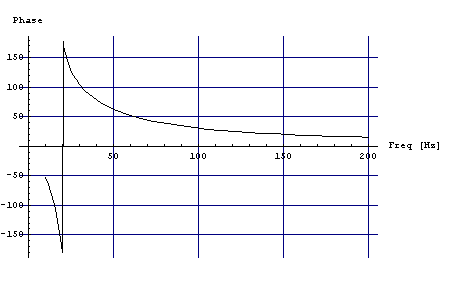
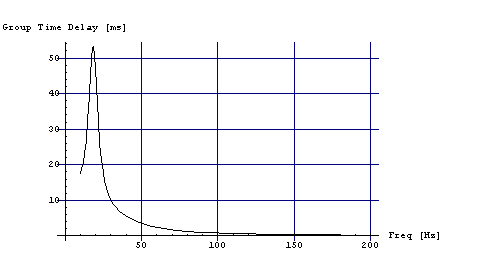
Рис. 4. Расчет ФИ по представленной модели.
Сравнение Рис.3 и Рис.4 показывает, что в обоих случаях («виброплата» и ФИ) ГВЗ имеет большое значение.
Сравнение "Виброплаты" с пассивным излучателем (ПИ).
На рис.5 показан расчет с пассивным излучателем (k=0). Графики немного отличаются от Рис.3. Т.е. эффект «Виброплаты» оказывает влияние на результат.
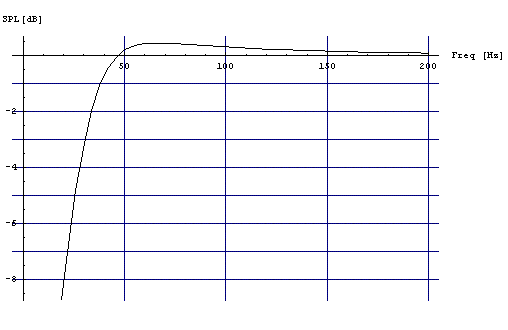
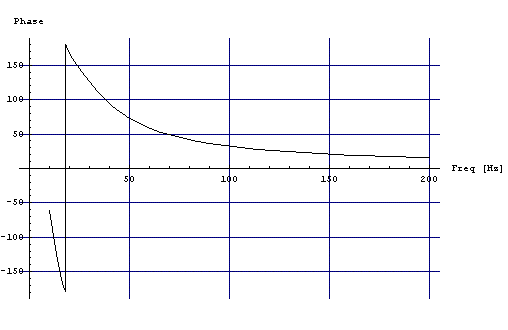
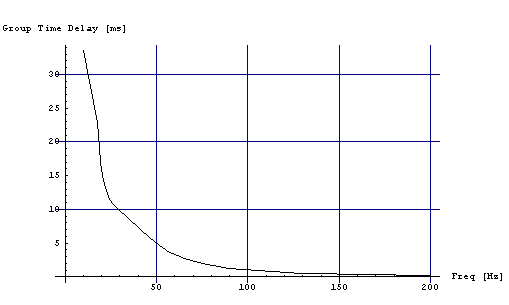
Рис. 5
Расчет "вариовента" (ПАС).
Наконец, в качестве последнего примера, покажем как с помощью данной модели рассчитать ПАС (вариовент). Для этого необходимо добавить порт и учесть конечное акустическое сопротивление в порту.
Расчет выполним на примере динамика 6гд2 в ящике 70 литров:
V=0.070;
Mms=0.015; [кг];
Cms=0.0015 [метр/ньютон];
Rms=0.52 [Ньютон×сек/метр];
B×L=5.1 [Тл×метр];
Sd=0.032 [кв м] - площадь диффузора;
Re=5.5 [Ом] - сопротивление катушки;
Отверстие выберем длиной L=0 и радиусом α=0.2 м.
В зависимости от акустического сопротивления в порту Z0 получаем семейство решений (Рис. 6) вплоть от полностью открытого порта (Z0=0) до ЗЯ (Z0 велико). Оптимальным оказывается промежуточное значение Z0.
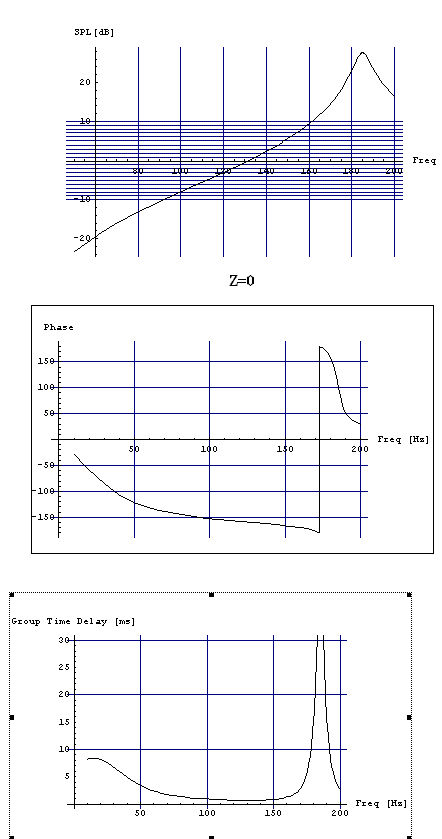
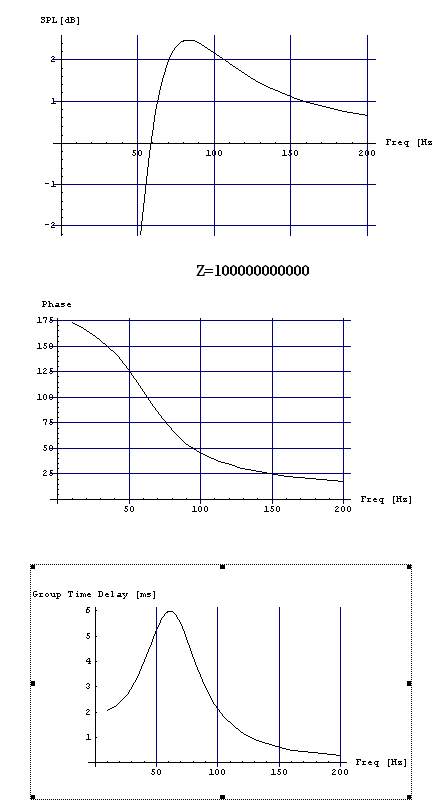
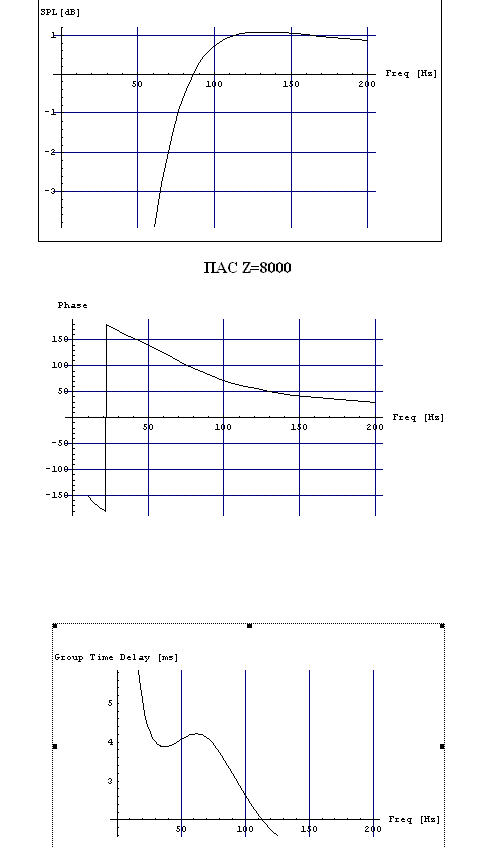
Рис. 6 Зависимость от Z0.
Заключение.
Автор надеется, что данная программа окажется полезным тем, кто захочет построит АС с «виброплатой». Программа также может оказаться полезной в расчете ПАС и ПИ.
А. Ю. Соколов
| 1 |
Добавлена новая версия соответствующего файла с расчетами, где были исправлены незначительные ошибки.
(15.11.2009, 08:09)
|
| 2 |

|
Грамотно проделанная работа, респект автору!
Подскажите, каким образом (формула) в проекте можно вывести график результирующего импеданса динамика,т.е. то что обычно измеряется в программах моделирования акустики. Или как связаться с автором. (01.02.2012, 10:31)
|
| 4 |
В самом начале статьи в описании движения диффузора и виброплаты и воздуха допущена ошибка. Если диффзор пошел вперед из ящика, то в ящике создается разрежение и направление движения виброплата внутрь ящика ( к ней ещё прикладывается сила отдачи, как, например у пистолета при выстреле), а на выходе фазоинвертора воздух будет вссасываться внутрь ящика (если не возникли резонансные явления). А если на эти предпосылки опираются все расчеты, то ???????????....
(09.11.2013, 05:29)
|
| 5 |
Все мы человеки и от ошибок никто не застрахован. Я так давно не согласен с выводами этой работы, т.к. мои практические наработки дают совсем другие результаты.)))
(09.11.2013, 05:46)
|
| 6 |

|
2 giv94 с опозданием...
это где это там допущена ошибка? в "картинке" что-ли? то есть текст не читали. зашибись. формулы для кого? знак "минус" для кого? "сила отдачи" епта... уравнение (2) почему содержит в правой части силу, а? учебник алгебры 8-9 классы в помощь. критикуя какую-то область, неплохо в этой области разбираться. вот alpert2003 по делу говорит. практика дает расхождение с теорией. что нормально для свежей теории. но он не напирает, что статья неправильная или в ней ошибки. математически статья верна. неучтенность каких-то высших членов или сторонних явлений - это одно, а "ошибочность" это совсем другое. (05.05.2014, 10:22)
|


